Ordenar es el proceso de ubicar elementos de una colección en algún orden. Por ejemplo, una lista de palabras podría ordenarse alfabéticamente o por longitud. Una lista de ciudades podría ordenarse por población, por área o por código postal. Ya hemos visto una serie de algoritmos que fueron capaces de beneficiarse de tener una lista ordenada (recuerde el ejemplo final del anagrama y la búsqueda binaria).

Se han desarrollado y analizado muchísimos algoritmos de ordenamiento. Esto sugiere que el ordenamiento es una importante área de estudio en las ciencias de la computación. Ordenar un gran número de elementos puede requerir una cantidad considerable de recursos informáticos. Al igual que la búsqueda, la eficiencia de un algoritmo de ordenamiento está relacionada con el número de elementos que se están procesando. Para las pequeñas colecciones, un método de ordenamiento complejo puede resultar más problemático que beneficioso. La sobrecarga puede ser demasiado alta. Por otra parte, para colecciones más grandes, queremos aprovechar tantas mejoras como sean posibles. En esta sección discutiremos varias técnicas de ordenamiento y las compararemos respecto a sus tiempos de ejecución.

Antes de considerar algoritmos específicos, debemos pensar en las operaciones que se pueden utilizar para analizar un proceso de ordenamiento. Primero, será necesario comparar dos valores para ver cuál es más pequeño (o más grande). Para ordenar una colección, será necesario contar con una manera sistemática de comparar los valores para ver si no están en orden. El número total de comparaciones será la forma más común de medir un procedimiento de ordenamiento. En segundo lugar, cuando los valores no están en la posición correcta con respecto a los otros, puede ser necesario intercambiarlos. Este intercambio es una operación costosa y el número total de intercambios también será importante para evaluar la eficiencia global del algoritmo.

El ordenamiento burbuja

El ordenamiento burbuja hace múltiples pasadas a lo largo de una lista. Compara los elementos adyacentes e intercambia los que no están en orden. Cada pasada a lo largo de la lista ubica el siguiente valor más grande en su lugar apropiado. En esencia, cada elemento “burbujea” hasta el lugar al que pertenece.

La Figura 1 muestra la primera pasada de un ordenamiento burbuja. Los elementos sombreados se comparan para ver si no están en orden. Si hay n elementos en la lista, entonces hay n−1n−1 parejas de elementos que deben compararse en la primera pasada. Es importante tener en cuenta que, una vez que el valor más grande de la lista es parte de una pareja, éste avanzará continuamente hasta que la pasada se complete.

Al comienzo de la segunda pasada, el valor más grande ya está en su lugar. Quedan n−1n−1 elementos por ordenar, lo que significa que habrá n−2n−2 parejas. Puesto que cada pasada ubica al siguiente valor mayor en su lugar, el número total de pasadas necesarias será n−1n−1. Después de completar la pasada n−1n−1, el elemento más pequeño debe estar en la posición correcta sin requerir procesamiento adicional.

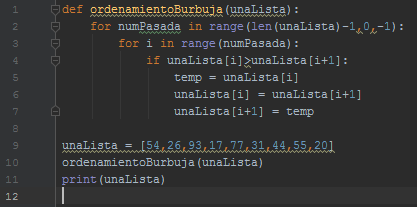
El Código muestra la función que llamaremos ordenamientoBurbuja completa. La función recibe la lista como un parámetro, y lo modifica intercambiando elementos según sea necesario.

La operación de intercambio es ligeramente diferente en Python que en la mayoría de los otros lenguajes de programación. Normalmente, el intercambio de dos elementos en una lista requiere una ubicación de almacenamiento temporal (una ubicación de memoria adicional). Un fragmento de código como

temp = unaLista[i]
unaLista[i] = unaLista[j]
unaLista[j] = temp

intercambiará los elementos ii-ésimo y jj-ésimo de la lista. Sin el almacenamiento temporal, uno de los valores sería sobrescrito.

En Python es posible realizar la asignación simultánea. La instrucción a,b=b,a dará lugar a que se realicen dos instrucciones de asignación al mismo tiempo (véase la Figura 2). Usando la asignación simultánea, la operación de intercambio se puede hacer en una sola instrucción.

Las líneas 5-7 en el Código realizan el intercambio de los elementos ii-ésimo e (i+1)(i+1)-ésimo utilizando el procedimiento de tres pasos descrito anteriormente. Note que también podríamos haber utilizado la asignación simultánea para intercambiar los elementos.

El siguiente ejemplo de Código muestra la función ordenamiento Burbuja completa operando sobre la lista mostrada arriba.

Realiza el ejercicio.

Ahora, es importante mencionar que un ordenamiento burbuja se considera frecuentemente como el método de ordenamiento más ineficiente ya que debe intercambiar elementos de la lista antes de que se conozca su ubicación final.

Estas operaciones de intercambio “desperdiciadas” son costosas, pero debido a que el ordenamiento burbuja hace pasadas por toda la parte no ordenada de la lista, tiene la capacidad de hacer algo que la mayoría de los algoritmos de ordenamiento no pueden: si durante una pasada no hubo intercambios, entonces sabemos que la lista ya debe estar ordenada.

Un ordenamiento burbuja se puede modificar para detenerse anticipadamente si encuentra que la lista ya ha sido ordenada. Esto significa que para las listas que requieran sólo unas pocas pasadas, un ordenamiento burbuja puede tener la ventaja de reconocer que la lista ya está ordenada y se detendrá.

El Código a continuación muestra esta modificación, que a menudo se conoce como el ordenamiento burbuja corto:

Como podemos apreciar, en la lista sólo esta desordenado el 90.

Realiza el ejercicio y prueba este código más eficiente.

El ordenamiento por selección

El ordenamiento por selección mejora el ordenamiento burbuja haciendo un sólo intercambio por cada pasada a través de la lista. Para hacer esto, un ordenamiento por selección busca el valor mayor a medida que hace una pasada y, después de completar la pasada, lo pone en la ubicación correcta. Al igual que con un ordenamiento burbuja, después de la primera pasada, el ítem mayor está en la ubicación correcta. Después de la segunda pasada, el siguiente mayor está en su ubicación. Este proceso continúa y requiere n−1n−1 pasadas para ordenar los n ítems, ya que el ítem final debe estar en su lugar después de la (n−1)(n−1)-ésima pasada.

La Figura 3 muestra todo el proceso de ordenamiento. En cada paso, el ítem mayor restante se selecciona y luego se pone en su ubicación correcta. La primera pasada ubica el 93, la segunda pasada ubica el 77, la tercera ubica el 55, y así sucesivamente. La función se muestra en el Código.